In an effort to understand machine learning from the ground up, the aim of this post is to implement a really simple machine learning system to help understand the fundamentals. “Univariate Linear Regression” is probably the simplest system to implement, it certainly isn’t the most effective for complex problems but its a good starting point to understanding machine learning.

• Training Data
• Linear Function
• Gradient Descent
• Cost Function (MSE)

Overview

In simple terms all we are trying to achieve, is to take the input data on the left and “fit” a line down the middle of the data points as accurately as possible.

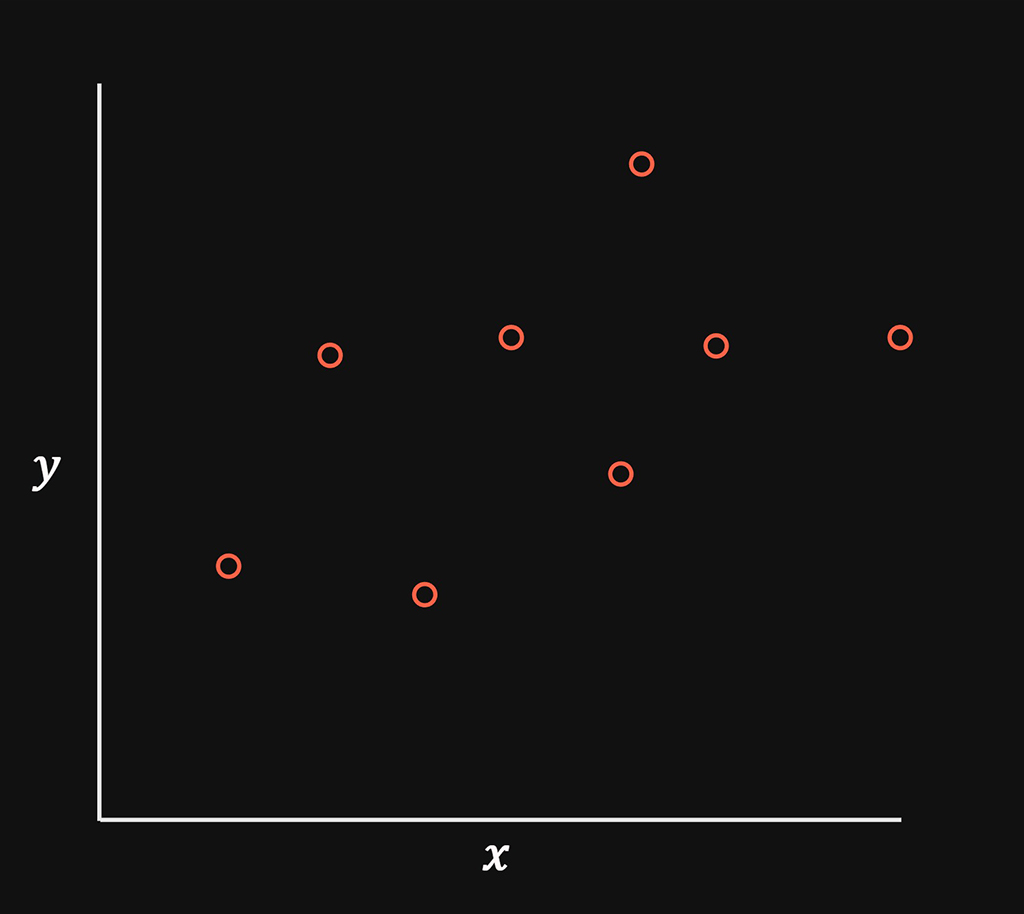
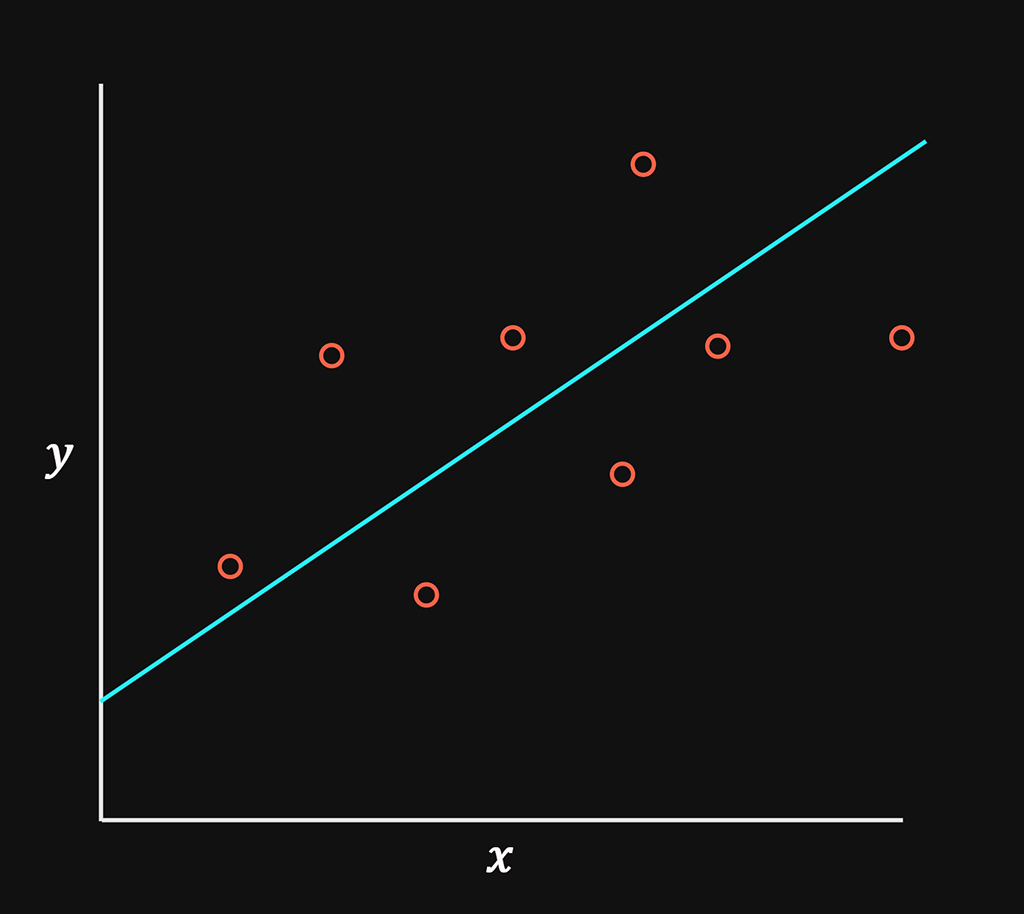
Linear regression is simply creating a straight line to represent existing data points as accurately as possible.

What this enables us to do , is provide a method of predicting any value along that straight line as a extrapolation of the input data. The line fills in the missing gaps of data, by approximating it.

Use Case:
Lets say you want to predict the house price based on a single variable. Lets call this variable \(x\) and it will represent the internal square footage of a property. Based on \(x\) the system will attempt to predict the sale price of the house. The output will be referred to as \(y\)

$$ x(ft^2) \rightarrow y(Sale \ Price) $$

The above represents the input or training data on the left and the outcome of the system will be the straight line on the right.

The training data is a sample of the correct relationship between \(x\) and \(y\), it provides the correct value of what \(y\) will be relative to \(x\) for the number of samples in the training data.
Since we are using input data that represents correct output data this system is a supervised learning system.
The input or training data will only have a limited number of correct “answers” of what the the sale price (\(y\)) will be when given the size of the property (\(x\)). What our system will provide us is the ability to get an sale price (\(y\)) estimation or prediction of any sized house (\(x\)) even if it falls outside of the data provided by the training data.

System Properties:

• Learning Type: Supervised
• Category: Regression (Linear)
• Properties: Univariate

Lets understand what this means in more detail.

Learning Type: Supervised

• The system uses supervised learning which means it will require labelled data that demonstrates examples of the correct outcome

Category: Regression

• A regression system is used to model the relationship between one or more input variables(features) to a single output variable (target)
• Linear meaning we will find a straight line that best fits a set of data points. This line will be used to predict target values that do not exist in the input data.

Properties: Univariate

• We will be using a single input variable (feature) as our training data, since we are only using one input feature we are working with a univariate system.

$$ x \rightarrow y $$

• If we had multiple input variables that are being used as training data , we would have a multivariate system.
• Batch
  

Implementation

I will be using python as my language of choice, first I will run the system on test data to established intuition of how it works in a controlled way. Once established I will run the same system on real housing data as a final test.

Training Data Representation (test data)

\(x\)	\(y\)
1	2
2	4
3	6
4	8
5	10

Model Representation

• \(m\) = Number of training data samples (test data = 5 rows)
• \(x\) = Input variable or input feature
• \(y\) = Output variable or target variable
• \((x^{(i)},y^{(i)});i=1,…,m\) = This represents the entire set of training data from 1 to 5.
• \(x=y=\mathbb{R}\)

Hypothesis

The hypothesis is the method of mapping or predicting the output values \(y\) given \(x\).

The term hypotheses is has been adopted as a convention, although its best not to over analysis the use here.

• Hypothesis = \(h\)
• \(h\) effectively produces \(y\) given \(x\).
• H is a function that converts any \(x\) input into the predicted value \(y\)

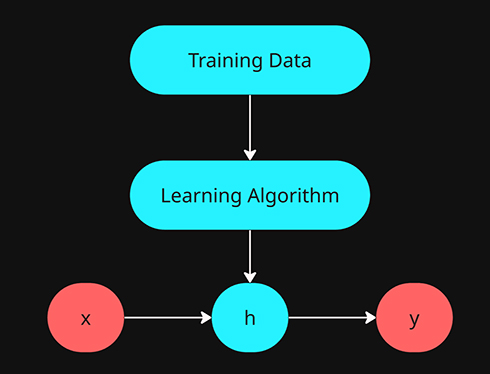
H representation

H will be represented by the following linear function.

$$h_{\theta}(x) = \theta_0 + \theta_1x$$

• This function produces a linear line that will be adjusted to best fit the training data set.
• The function takes \(x\) as input and produces the \(y\) output value.
• Shorthand: \(h(x)\)
• \(\theta_0 \ \& \ \theta_1\): These are the two parameters the system will adjust to increase the alignment of the straight line to the data set. Which will in turn produce more accurate predictions.

Cost Function

The cost function measures how close the line is to aligning with the training data set. Its a measure of the distance from the line represented by \(h\) to the \(y\) values in the training data.

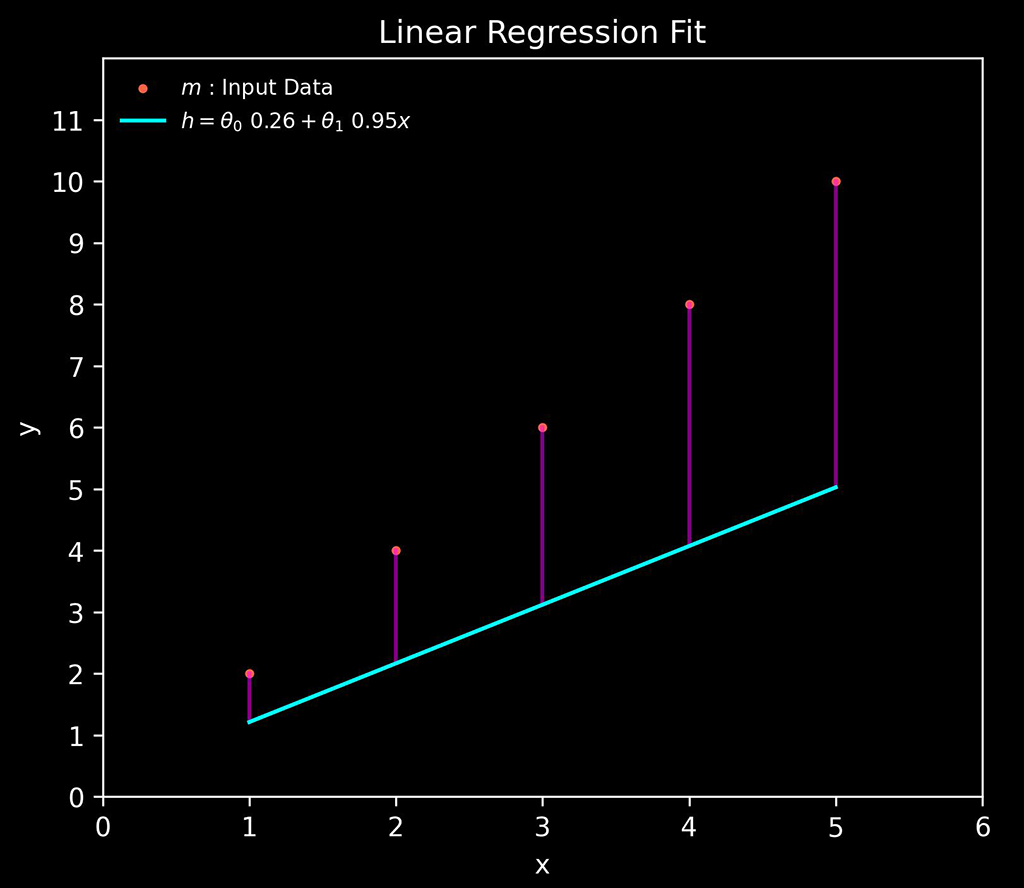
In the above chart, there are three main things to note:

• Input Training Data: Red dots
• Linear function (\(h)\): Cyan line
• Error: Purple lines

The training data is out test data taken from the previous table above. The cyan line is our hypothesis (\h\) which is the linear function and the error is the distance between the position of the linear function and the input data set.

The cost function is the measure of the amount of error between the hypothesis function and the input data. The smaller the cost function or error, the more accurate the system will be at predicting the output value \(y\). This cost function is how we measure the performance of the learning algorithm.

Cost Function Formular:

Type: Mean Squared Error (MSE)

$$\frac{1}{m}\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^2$$

lets break this down:

• \(h_{\theta}(x^{(i)})-y^{(i)}\): \(h_{\theta}(x^{(i)})\) This is the linear function that represents the line we are trying to fit. For each \(x\) value found in our training data we producing a predicted (\hat{y}\) value based on the linear function, from here we are subtracting the real \(y\) value found in the training data. This gives us the delta between the predicted \(\hat{y}\) and the “real” input data \(y\). This delta represents the error between where the linear function is and where it should be.
• The delta calculated from the above is squared which either reduces a smaller error or exaggerates larger errors.
• This squared error is calculated for every row found in the training data and added together before being averaged via the multiplication of \(\frac{1}{m}\).
• This is know as the Mean Squared Error (MSE)

$$E=mc^2$$

Euler’s identity: \(e^{i\pi} + 1 = 0\)

$$2^2$$

\(e^{i\pi} + 1 = 0\)